原理解读
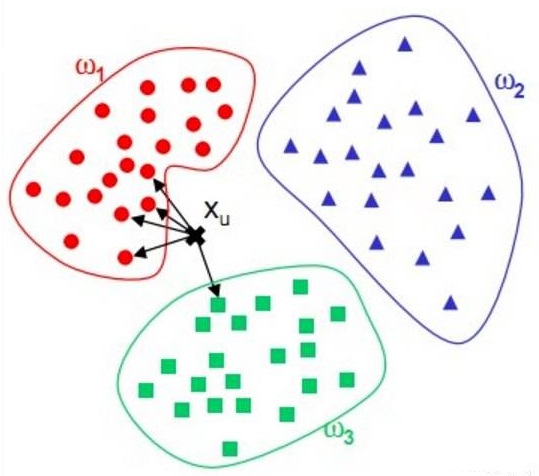
KNN(K Nearest Neighbor):又称K近邻,是一种基本分类方法,给定测试实例,基于某种距离度量找出训练集中与其最靠近的k个实例点,然后基于这k个最近邻的信息使用投票法,即选择这k个实例中出现最多的标记类别作为分类结果。
核心思想
距离的度量
1. 欧式距离(Euclidean Distance)
$$L_2(x_i,x_j)=\sqrt{\displaystyle \sum_{k=1}^n ({x_i}^{(k)}-{x_j}^{(k)})^2}$$
2. 曼哈顿距离(Manhattan distance)
$$L_1(x_i,x_j)=\displaystyle \sum_{k=1}^n \lvert{x_i}^{(k)}-{x_j}^{(k)} \rvert$$
3.余弦距离(Cosine Distance)
$$L_{cos}(x_i,x_j)=1-\frac{x_i \cdot x_j}{\lVert x_i \rVert_2 \ \lVert x_j \rVert_2}$$
K值的选择
K值的选择会对K近邻法的结果产生重大影响,在应用中,k值一般取一个比较小的数值,通常采用交叉验证法来选取最优的k值。
K=1时K近邻算法退化成最近邻,即数据的类别为距离最近的样本的类别。
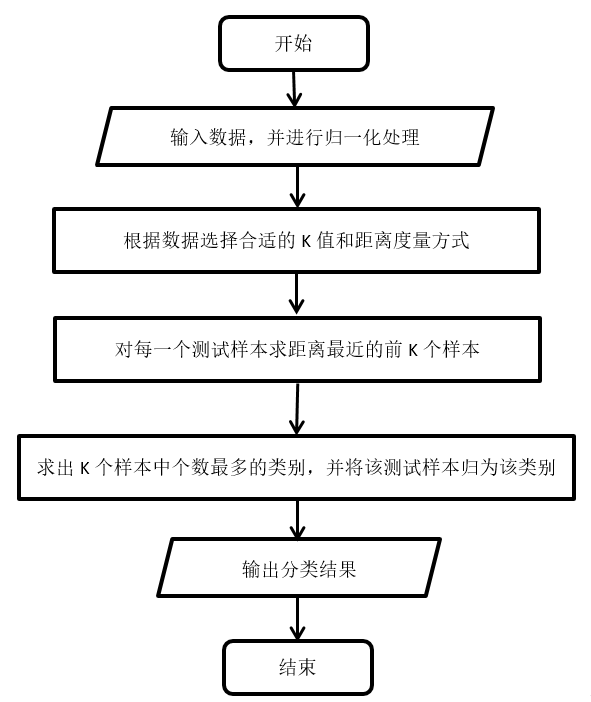
算法流程
代码实战
KNN_main.m
1 | clear;clc;close all; |
KNN_classify.m
1 | function test_y=KNN_classify(train_x_scale,train_y,test_x_scale,train_num,test_num,knn) |
KNN_display.m
1 | function KNN_display(train_x,train_y,test_x,test_y,train_num,test_num,class_num) |
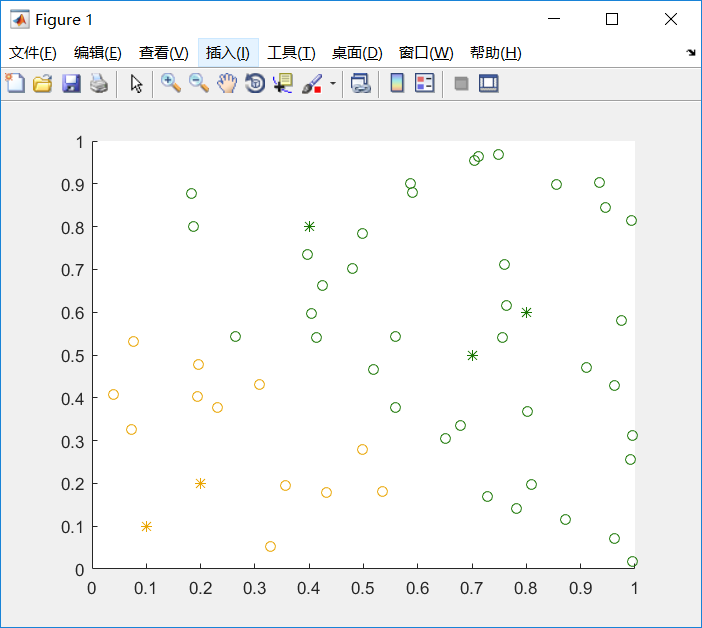
实验结果
KNN优缺点
- 优点:
- 无需参数估计,无需训练
- 算法简单,易于理解和实现
- 适合于对稀有数据进行分类
- 特别适合于多分类问题,KNN的表现超过SVM
- 缺点:
- 无法给出分类规则
- 对于高维特征,距离的选择和衡量不准确
- 计算量较大,对每一个测试样本都需要计算与其他样本的距离
- 样本不平衡时,尤其是一类样本多,其他类样本少时会产生严重的问题